Các phương pháp chứng minh hình học thường gặp
☼ Cách chứng minh hai đoạn thẳng bằng nhau
1. C/m 2 tam giác chứa 2 đoạn thẳng đó bằng nhau
2. C/m 2 đoạn thẳng đó là 2 cạnh bên của tam giác cân
3. C/m 2 đoạn thẳng đó cùng bằng 1 đại lượng thứ 3
4. C/m 2 đoạn thẳng đó là 2 cạnh đối của hình bình hành, hình chữ nhật, hình thoi, hình vuông hoặc là 2 đường chéo của hình thang cân, hình chữ nhật, hình vuông hay 2 cạnh bên của hình thang cân
5. C/m bằng phương pháp cộng đoạn thẳng
6. C/m dưa vào tính chất đường trung trực của đoạn thẳng
☼ Cách chứng minh hai góc bằng nhau
1. C/m 2 góc đó là 2 góc tương ứng của 2 tam giác bằng nhau hoặc 2 tam giác đồng dạng
2. C/m 2 góc đó là 2 góc cùa 1 tam giác cân
3. C/m 2 góc đó cùng bằng hoặc cùng bù hoặc cùng phụ với góc thứ 3
4. C/m 2 góc này ở vị trí SLT hoặc ÑV của 2 đường thẳng song song và 1 cát tuyến
5. C/m 2 góc đó là 2 góc đáy của hình thang cân, 2 góc đối của hình bình hành, hình chữ nhật, hình thoi…
6. C/m dựa vào tính chất tia phân giác của 1 góc
☼ Cách chứng minh hai tam giác bằng nhau
* C/m hai tam giác thường bằng nhau
1. C/m theo trường hợp cạnh – góc – cạnh ( c – g- c)
2. C/m theo trường hợp góc – cạnh – góc ( g- c –g )
3. C/m theo trường hợp cạnh – cạnh- cạnh ( c – c – c)
** C/m hai tam giác vuông bằng nhau
1. C/m theo trường hợp bằng nhau của 2 tam giác thường
2.C/m theo trường hợp đặc biệt : cạnh huyền – góc nhọn hoặc cạnh huyền – cạnh g.vuông
☼ Cách chứng minh hai đường thẳng song song
1. C/m 2 góc tạo bởi 2 đường thẳng đó và 1 cát tuyến ở vị trí so le trong bằng nhau hoặc dồng vị bằng nhau hoặc trong cùng phía bù nhau
2. C/m 2 đường thẳng đó cùng song song hay cùng vuông góc với đường thẳng thứ 3
3. C/m 2 đường thẳng đó chứa 2 cạnh đối của hình bình hành , hình thoi, hình chữ nhật, hình vuông..
4. C/m dựa vào tính chất đường trung bình của tam giác
5. C/m dựa vào định lý Ta let đảo
☼ Cách chứng minh hai đường thẳng vuông góc
1. C/m góc tạo bởi 2 đường thẳng đó là góc vuông
2. C/m dựa vào tính chất của 2 đường thẳng song song: Nếu a // b và b vuông góc c. Suy ra: a vuông góc c
3. C/m dựa vào tính chất của tam giác cân : Trong tam giác cân thì đường trung tuyến hay đường phân giác đồng thời là đường cao
4. C/m dựa vào tính chất trực tâm tam giác : Trong tam giác thì đoạn thẳng nối từ đỉnh đến trực tâm tam giác thì vuông góc với cạnh đối diện
5. C/m 2 đường thẳng đó là 2 đường chéo của hình thoi hay hình vuông
6. C/m dựa vào tính chất đường trung trực của đoạn thẳng
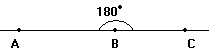
1. C/m :góc ABC=1800 . Suy ra: A,B,C thẳng hàng
2. C/m 2 đường thẳng cùng đi qua một điếm và cùng vuông góc hoặc cùng song song với 1 đường thẳng thứ 3
3. C/m dựa vào tính chất 2 đường chéo của hình bình hành, hình thoi, hình chữ nhật, hình vuông
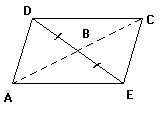
VD: Tứ giác ADCE là hình bình hành có:
B là trung điểm của đường chéo DE
Nên: B cũng là trung điểm của đường chéo AC
Suy ra: A,B,C thẳng hàng
4. C/m 3 điểm đó cùng thuộc đường trung trực của 1 đoạn thẳng
5. C/m dựa vào tính chất 3 đường cao, 3 đường trung tuyến, 3 đường phân giác trong tam giác đồng qui tại một điểm
☼ Chứng minh ba đường thẳng đồng qui
1. C/m dựa vào tính chất các đường đồng qui trong tam giác:
Trong tam giác 3 đường cao, 3 đường trung tuyến, 3 đường phân giác, 3 đường trung trực gặp nhau tại 1 điểm
2. C/m một trong 3 đường thẳng đi qua giao điểm của 2 đường thẳng còn lại hay giao điểm của 2 đường thẳng và 2 điểm nằm trên đường thẳng thứ 3 thẳng hàng
☼ Chứng minh đường thẳng là trung trực của đoạn thẳng
1. C/m : Đường thẳng đó vuông góc với đoạn thẳng tại trung điểm của nó
2. C/m : 2 điểm nằm trên đường thẳng đó cách đều 2 đầu đoạn thẳng đã cho
3. C/m dựa vào tính chất của tam giác cân: Trong tam giác cân đường trung tuyến hoặc đường cao hoăc đường phân giác thuộc cạnh đáy là đường trung trực của cạnh đáy
☼ Chứng minh tam giác cân
1. C/m tam giác có 2 cạnh hoặc 2 góc bằng nhau
2. C/m dựa vào tính chất: Trong 1 tam giác nếu đường cao cũng là phân giác hoặc đường cao cũng là trung tuyến thì tam giác đó là tam giác cân . Tương tự đối với đường phân giác và trung tuyến…
☼ Chứng minh tam giác đều
1. C/m tam giác có 3 cạnh bằng nhau hoặc có 3 góc bằng nhau
2. C/m tam giác cân có 1 góc 600
☼ Chứng minh tam giác vuông
C/m tam giác có 1 góc vuông hay tam giác có 2 góc nhọn có tổng bằng 900
2. C/m dựa vào định lý Pitago đảo
3. C/m tam giác có đường trung tuyến thuộc 1 cạnh bằng nửa cạnh đó
☼ Chứng minh tứ giác là hình thang cân
1. C/m hình thang có 2 góc kề 1 đáy bằng nhau
2. C/m hình thang có 2 đường chéo bằng nhau
☼Chứng minh tứ giác là hình bình hành
1. C/m tứ giác có 2 cặp cạnh song song
2. C/m tứ giác có 2 cặp cạnh đối bằng nhau
3. C/m tứ giác có 2 cặp góc đối bằng nhau
4. C/m tứ giác có 1 cặp cạnh đối vừa song song vừa bằng nhau
5. C/m tứ giác có 2 đường chéo cắt nhau tại trung điểm của mỗi đường
☼ Chứng minh tứ giác là hình chữ nhật
1. C/m tứ giác có 3 góc vuông
2. C/m hính bình hành có 1 góc vuông
3. C/m hình bình hành có 2 đường chéo bằng nhau
4. C/m hình thang cân có 1 g.vuông
☼ Chứng minh tứ giác là hình thoi
1. C/m tứ giác có 4 cạnh bằng nhau
2. C/m hình bình hành có 2 cạnh kề bằng nhau
3. C/m hình bình hành có 2 đường chéo vuông góc
4. C/m hình bình hành có 1 đường chéo là đường phân giác của 1 góc
☼ Chứng minh tứ giác là hình vuông
1. C/m hình chữ nhật có 2 cạnh kề bằng nhau
2. C/m hình chữ nhật có 2 đường chéo vuông góc
3. C/m hình chữ nhật có 1 đường chéo là đường phân giác của 1 góc
4. C/m hình thoi có 2 góc vuông
5. C/m hình thoi có 2 đường chéo bằng nhau.