20 BÀI TOÁN TỨ GIÁC NỘI TIẾP TRONG ĐƯỜNG TRÒN – PHẦN 1

Bài 1: Cho(O) đường kính AC. trên đoạn OC lấy điểm  B và vẽ đường tròn tâm O’, đường kính BC. Gọi M là trung điểm của đoạn AB. Từ M vẽ dây cung DE vuông góc với AB;DC cắt đường tròn tâm O’ tại I.

                 1. Tứ giác ADBE là hình gì?

                 2. C/m DMBI nội tiếp.

                 3. C/m B;I;E thẳng hàng và MI=MD.

                 4. C/m MC. DB=MI. DC

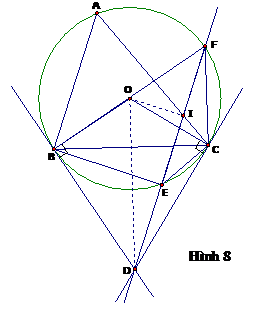
Bài 2: Cho (O) đường kính BC,điểm A nằm trên cung BC. Trên tia AC lấy điểm D sao cho AB=AD. Dựng hình vuông ABED;AE cắt (O) tại điểm thứ hai F;Tiếp tuyến tại B cắt đường thẳng DE tại G.

1. C/m BGDC nội tiếp. Xác định tâm I của đường tròn này.
2. C/m DBFC vuông cân và F là tâm đường tròn ngoại tiếp DBCD.
3. C/m GEFB nội tiếp.
4. Chứng tỏ:C;F;G thẳng hàng và G cùng nằm trên đường tròn ngoại tiếp DBCD. Có nhận xét gì về I và F

Tải tài liệu này tại đây. Đặt mua Sách tham khảo toán 9 tại đây! Tải bản WORD tại đây.