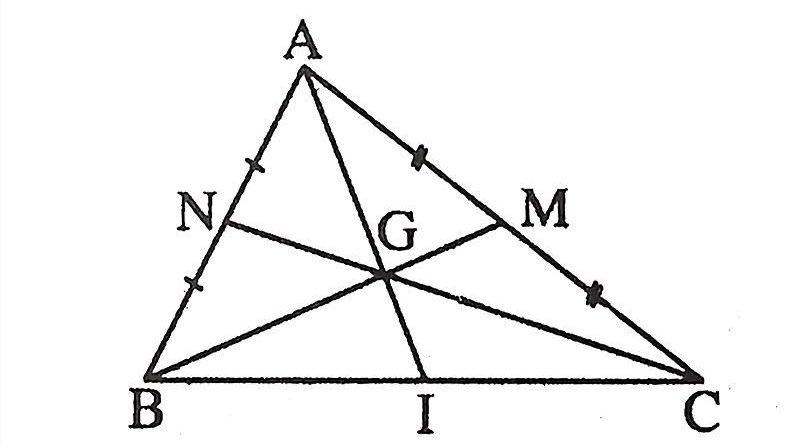
BÀI TẬP BA ĐƯỜNG TRUNG TUYẾN TRONG TAM GIÁC- HÌNH HỌC 7
Bài tập 1: Cho tam giác DEF cân tại D có đường trung tuyến DI.
a) Chứng minh : ΔDEI = ΔDFI.
b) Các góc DIE và góc DIF là góc gì ?
c) DE = DF = 13cm, EF = 10cm. tính DI.
Bài tập 2: Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của MA lấy điểm D sao cho MD = MA.
a) Tính số đo góc ABD
b) Chứng minh : ABC = BAD.
c) So sánh độ dài AM và BC.
Tải tài liệu này tại đây. Đặt mua Sách tham khảo toán 7 tại đây! Tải bản WORD tại đây.
Bài tập 3: Cho tam giác ABC nhọn (AB < AC), đường trung tuyến AM. Trên tia đối của MA lấy điểm D sao cho MD = MA.
a) Chứng minh : ΔAMB =ΔDMC và AB // CD.
b) Gọi F là trung điểm CD. tia FM cắt AB tại K. Chứng minh : M là trung điểm KF.
c) Gọi E là trung điểm của AC. BE cắt AM tại G, I là trung điểm của AF. Chứng minh : 3 điểm K, G và I thẳng hàng.
Bài tập 4: Cho tam giác ABC vuông tại A, có AB = 8cm, BC = 10cm.trung tuyến AD cắt trung tuyến BE ở G.
- Tính AC, AE.
- Tính BE, BG.
Bài tập 5: Giả sử hai đường trung tuyến BD và CE của tam giác ABC có độ dài bằng nhau và cắt nhau tại G.
- Tam giác BGC là tam giác gì ?
- So sánh tam giác BCD và tam giác CBE.
- Tam giác ABC là tam giác gì ?
Bài tập 6: Cho tam giác ABC có BC = 2BA. BD là đường phân giác. Chứng minh : CD = 2DA.
Bài tập 7: Hai đường trung tuyến AD và BE của tam giác ABC cắt nhau tại G. kéo dài GD thêm một đoạn DI = DG. Chứng minh : G là trung điểm của AI.
Bài tập 8: Trên đường trung tuyến AD của tam giác ABC, lấy hai điểm I và G sao cho AI = IG = GD. Gọi E là trung điểm của AC.
- Chứng minh B, G, E thẳng hàng và so sánh BE và GE.
- CI cắt GE tại O. điểm O là gì của tam giác ABC. chứng minh BE = 9OE.
Bài tập 9: Cho tam giác ABC vuông tại A có AB = 8cm, BC = 10cm. lấy điểm M trên cạnh AB sao cho BM = 4cm. lấy điểm D sao cho A là trung điểm của DC.
- Tính AD.
- Điểm M là gì của tam giác BCD.
- Gọi E là trung điểm của BC. chứng minh D, M, E thẳng hàng.
Bài tập 10: Cho tam giác DEF cân tại D có đường trung tuyến DI.
a) Chứng minh : ΔDEI = ΔDFI.
b) Các góc DIE và góc DIF là góc gì ?
c) DE = DF = 13cm, EF = 10cm. tính DI.
Bài tập 11: Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của MA lấy điểm D sao cho MD = MA.
a) Tính số đo góc ABD
b) Chứng minh : ABC = BAD.
c) So sánh độ dài AM và BC.
Bài tập 12: Cho tam giác ABC nhọn (AB < AC), đường trung tuyến AM. Trên tia đối của MA lấy điểm D sao cho MD = MA.
a) Chứng minh : ΔAMB =ΔDMC và AB // CD.
b) Gọi F là trung điểm CD. tia FM cắt AB tại K. Chứng minh : M là trung điểm KF.
c) Gọi E là trung điểm của AC. BE cắt AM tại G, I là trung điểm của AF. Chứng minh : 3 điểm K, G và I thẳng hàng.
Bài tập 13: Cho tam giác ABC vuông tại A, có AB = 8cm, BC = 10cm.trung tuyến AD cắt trung tuyến BE ở G.
- Tính AC, AE.
- Tính BE, BG.
Bài tập 14: Giả sử hai đường trung tuyến BD và CE của tam giác ABC có độ dài bằng nhau và cắt nhau tại G.
- Tam giác BGC là tam giác gì ?
- So sánh tam giác BCD và tam giác CBE.
- Tam giác ABC là tam giác gì ?
Bài tập 15: Cho tam giác ABC có BC = 2BA. BD là đường phân giác. Chứng minh : CD = 2DA.
Bài tập 16: Hai đường trung tuyến AD và BE của tam giác ABC cắt nhau tại G. kéo dài GD thêm một đoạn DI = DG. Chứng minh : G là trung điểm của AI.
Bài tập 17: Trên đường trung tuyến AD của tam giác ABC, lấy hai điểm I và G sao cho AI = IG = GD. Gọi E là trung điểm của AC.
- Chứng minh B, G, E thẳng hàng và so sánh BE và GE.
- CI cắt GE tại O. điểm O là gì của tam giác ABC. chứng minh BE = 9OE.
Bài tập 18: Cho tam giác ABC vuông tại A có AB = 8cm, BC = 10cm. lấy điểm M trên cạnh AB sao cho BM = 4cm. lấy điểm D sao cho A là trung điểm của DC.
- Tính AD.
- Điểm M là gì của tam giác BCD.
- Gọi E là trung điểm của BC. chứng minh D, M, E thẳng hàng.