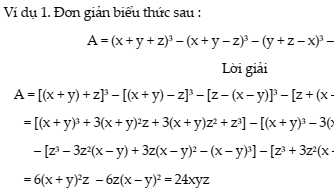Chuyên đề i: Biến đổi biểu thức đại số- Phần 1

Tải tài liệu này tại đây. Đặt mua Sách tham khảo toán 8 tại đây! Tải bản WORD tại đây.

Trích dẫn có trong tài liệu:

I.  Một số hằng đẳng thức cơ bản

1. (a ± b)² = a² ± 2ab + b² ;

(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca ;

 = ;

• (a ± b)³ = a³ ± 3a²b + 3ab² ± b³  = a³ ± b³ ± 3ab(a ± b);

     (a ± b)⁴ = a⁴ ± 4a³b + 6a²b² ± 4ab³ + b⁴ ;

• a² – b² = (a – b)(a + b) ;

a³ – b³ = (a – b)(a² + ab + b²) ;

aⁿ – bⁿ = (a – b)(a^{n – 1} + a^{n – 2}b + a^{n – 3}b² + … + ab^{n – 2} + b^{n – 1}) ;

• a³ + b³ = (a + b)(a² – ab + b²)

a⁵ + b⁵ = (a + b)(a⁴ – a³b + a²b² – ab³ + b⁵) ;

a^{2k + 1} + b^{2k + 1} = (a + b)(a^2k – a^{2k – 1}b + a^{2k – 2}b² – … + a²b^{2k – 2} – ab^{2k – 1} + b^2k) ;

II.  Các ví dụ

 Ví dụ 1. Đơn giản biểu thức sau :

A = (x + y + z)³ – (x + y – z)³ – (y + z – x)³ – (z + x – y)³.

Lời giải

    A = [(x + y) + z]³ – [(x + y) – z]³ – [z – (x – y)]³ – [z + (x – y)]³

       = [(x + y)³ + 3(x + y)²z + 3(x + y)z² + z³] – [(x + y)³ – 3(x + y)²z + 3(x + y)z² – z³] –

          – [z³ – 3z²(x – y) + 3z(x – y)² – (x – y)³] – [z³ + 3z²(x – y) + 3z(x – y)² + (x – y)³]

       = 6(x + y)²z  – 6z(x – y)² = 24xyz     

 Ví dụ 2. Cho x + y = a, xy = b (a² ≥ 4b). Tính giá trị của các biểu thức sau :

   a) x² + y² ;                  b) x³ + y³ ;                      c) x⁴ + y⁴ ;                     d) x⁵ + y⁵

Lời giải

1. x² + y² = (x + y)² – 2xy = a² – 2b
2. x³ + y³ = (x + y)³ – 3xy(x + y) = a³ – 3ab
3. x⁴ + y⁴ = (x² + y²)² – 2x²y² = (a² – 2b)² – 2b² = a⁴ – 4a²b + 2b²
4. (x² + y²)(x³ + y³) = x⁵ + x²y³ + x³y² + y⁵ = (x⁵ + y⁵) + x²y²(x + y)

Hay : (a² – 2b)(a³ – 3ab) = (x⁵ + y⁵) + ab² Þ x⁵ + y⁵ = a⁵ – 5a³b + 5ab²

    Chú ý : a⁶ + b⁶ = (a²)³ + (b²)³ = (a³)² + (b³)²

                   a⁷ + b⁷ = (a³ + b³)(a⁴ + b⁴) – a³b³(a + b)

                             = (a² + b²)(a⁵ + b⁵) – a²b²(a³ + b³)

 Ví dụ 3. Chứng minh các hằng đẳng thức :

1. a³ + b³ + c³ – 3abc = (a + b + c)(a² + b² + c² – ab – bc – ca) ;
2. (a + b + c)³ – a³ – b³ – c³ = 3(a + b)(b + c)(c + a)

Lời giải

1. a³ + b³ + c³ – 3abc = (a + b)³ + c³ – 3abc – 3a²b – 3ab²

         = (a + b + c)[(a + b)² – (a + b)c + c²] – 3ab(a + b + c)

         = (a + b + c) [(a + b)² – (a + b)c + c² – 3ab]

         = (a + b + c)(a² + b² + c² – ab – bc – ca)                           

• (a + b + c)³ – a³ – b³ – c³ = [(a + b + c)³ – a³] – (b³ + c³)

= (b + c)[(a + b + c)² + (a + b + c)a + a²] – (b + c)(b² – bc + c²)

= (b + c)(3a² + 3ab + 3bc + 3ca) = 3(b + c)[a(a + b) + c(a + b)]

= 3(a + b)(b + c)(c + a)

 Ví dụ 4. Phân tích biểu thức sau thành nhân tử :

A = x³ – 3(a² + b²)x + 2(a³ + b³)

Lời giải

    Đặt S = a + b và P = ab, thì a² + b² = ; a³ + b³ = . Vì vậy :

    A = x³ – 3()x + 2() =

        = (x – a – b)[x² + (a + b)x – 2(a + b)² + 6ab]

        = (x – a – b)[x² + (a + b)x – 2(a²

  Ví dụ 5. Cho x + y + z = 0. Chứng minh rằng : 2(x⁵ + y⁵ + z⁵) = 5xyz(x² + y² + z²)

Lời giải

     Vì  x + y + z = 0 nên x + y = –z Þ (x + y)³ = –z³

     Hay x³ + y³ + 3xy(x + y) = –z³ Þ 3xyz = x³ + y³ + z³

     Do đó : 3xyz(x² + y² + z²) = (x³ + y³ + z³)(x² + y² + z²)

                                             = x⁵ + y⁵ + z⁵ + x³(y² + z²) + y³(z² + x²) + z³(x² + y²)

     Mà x² + y² = (x + y)² – 2xy = z² – 2xy (vì x + y = –z). Tương tự :

              y² + z² = x² – 2yz ; z² + x² = y² – 2zx.

     Vì vậy : 3xyz(x² + y² + z²) = x⁵ + y⁵ + z⁵ + x³(x² – 2yz) + y³(y² – 2zx) + z³(z³ – 2xy)

                                                         = 2(x⁵ + y⁵ + z⁵) – 2xyz(x² + y² + z²)     

     Suy ra : 2(x⁵ + y⁵ + z⁵) = 5xyz(x² + y² + z²) (đpcm)